軌跡

拋物線

我們來做一條拋物線吧!

  1. 畫一條直線 PQ 當做拋物線的準線。
  2. 線外隨便畫一點 F 當做拋物線的焦點。
  3. 在直線 PQ 上面任取一點 S (請避開 P 與 Q)。 它是一個一維的自由點 (DOF=1)。 (P 與 Q 都是二維的自由點)。
  4. 過 S 做直線 PQ 的垂直線 L。

暫停一下。 回憶拋物線的定義, 現在我們希望在 L 上面找到一點 T, 它到準線的距離等於它到焦點的距離。 請想一下如何找出此點。

將來找出 T 之後, 只要移動 S, 就會看到 T 跟著動。 事實上隨著 S 在 L 上移動, T 就會畫出拋物線的軌跡。 等一下我們要用的 「幾何軌跡」 (Geometric Locus) 選單, 功能正是如此 -- 指定 S 為自變量, T 為應變量, 它就自動對 S 跑一個迴圈, 計算出 S 移到各處時, 相對應的 T 分別落在何等, 從而畫出拋物線。

OK, 剛才的問題, 要公佈答案了, 如果不想輕易放棄思考的機會, 請不要往下看。

  1. 連結線段 SF, 做它的中垂線 M, 與直線 L 相交即得 T。 拋物線
  2. 選取 「曲線」 (Curve) ==> 「幾何軌跡」 (Geometric Locus), 點選 S 為自變量, T 為應變量。
  3. 化妝一下, 把不要的線藏起來, 並且記得存檔吧!

凹凸透鏡成像原理

還記得小時候學的 「凹凸透鏡成像原理」 嗎?

  1. 平行於透鏡軸線的光線, 在通過透鏡時會轉向。 新的方向 (或其背後的延伸方向) 會通過透鏡的焦點。
  2. 通過透鏡中心的光線, 方向不變。

根據這兩點原則, 很容易可以推測出任何一點經過透鏡折射後的成像位置。

[凸透鏡成像原理] [凹透鏡成像原理]

  1. 過原點 O 畫一條水平線 H 。 並不需要畫得很平; 不過如果覺得看完全水平的水平線比較舒服的話, 可以用 「更改物件屬性」 ("change the property of an object", 在左側常用工具內, 或在 「數值」 子選單下) 手動替直線的兩點輸入相同的 y 座標。
  2. 過 O 畫一條垂直線 V。 我們想像透鏡放在 O, 鏡面落在 V, 軸線落在 H。
  3. H 上任取一點 F 當做焦點。
  4. 隨意畫一個圓 C 當做小人的頭, 在 C 上取一點 S 當做自變量。
  5. 根據上述原則畫出 S 成像的位置 T。
  6. 以 S 為自變量, T 為應變量, 畫出軌跡 C' 即為 C 像。
  7. 在 C 下面加上幾條簡單線段當做身體與手腳, 如法炮製, 求出這些線段的像。
  8. 拉動小人, 看看它的像如何變化? 移動焦點 F, 看看成像如何變化?

透鏡成像問題的解答

「最簡指令集」 觀點

玩 drgeo 的數學家可能會思考 "最簡指令集" 的問題: 選單裡面那些功能其實可以由其他功能組合完成? 換句話說, 有那些功能的用途純粹是簡化步驟, 但並不增加 drgeo 的作圖能力? 反過來問, 真正最重要, 無可取代的功能有那些? 如果我們逐一開放這些 "最簡指令", 則每增加某一項功能, 將可以讓我們多畫出那類的圖?

筆者不是數學家, 無法嚴謹地回答上面的問題; 只能做一點直覺, 簡單的觀察。 首先, 最重要的指令當然是畫點, 畫各種直線/線段, 及畫圓。 其他多數功能都可以用這幾項做出來。 例如要畫線段的垂直平分線, 可以用線段的兩端分別當圓心, 線段作為半徑, 畫兩個圓, 它們交點的連線就是原線段的垂直平分線。 第一篇的範例與題目都落在這個範圍內。

增加了 「軌跡」 功能, 我們馬上就想到可以畫二次曲線, 這是因為拋物線, 橢圓, 雙曲線都有很簡單的幾何定義。 事實上因為四則運算都可以用尺規方式作圖, 所以如果用代數的方式來思考, 應該是任何有理函數都可以畫 (多項式除以多項式)。

再來, 選單當中有一個不起眼的功能: 數值 (Numerical) ==> 角度 (Angle) 可以用來度量角度。 這個功能一放進來, 可以畫的東西就突然多了很多: 例如三角函數與極座標定義出來的某些曲線。 這是下一節的重點。

最後, 如果使用者可以自行撰寫程式, 那麼可以畫的圖就近乎沒有限制了。 後面的 Scripting 那一篇要探討的就是這個功能。

量角器開拓的新境界

我們先看看如何畫 sin(x) 函數。

  1. 畫水平線 OO' , 並在線上任選一點叫做 X。 OX 將當做單位長度。
  2. 以 O 為圓心, OX 為半徑, 畫一個單位圓, 並在圓上任選一點叫做 T。
  3. 畫出向量 OX 與 OT, 並丈量它們之間的有向角 (OX,OT)。
  4. 用 "變換 (transformation)" ==> "平移 (translation)" 把 O' 平移 OX, 得到 X'。
  5. 用 "變換 (transformation)" ==> "縮放 (scale)" 以 O' 為原點, 把 X' 縮放 (OX,OT) 倍, 得到 Ax。 (注意視窗最下列的訊息: 要先點 X', 次點 O', 最後點角 (OX,OT)。) 注意此時 drgeo 採用弳度量 (radian) 而不是度數 (degree)。 所以它所產生的倍數效果是 -3.1416 到 3.1416 而不是 -180 倍到 180 倍。
  6. 過 Ax 做 OO' 的垂直線; 過 T 做 OO' 的平行線; 兩者交於 A。
  7. 以 T 為自變量, A 為應變量, 畫出來的軌跡就是 sin(x)

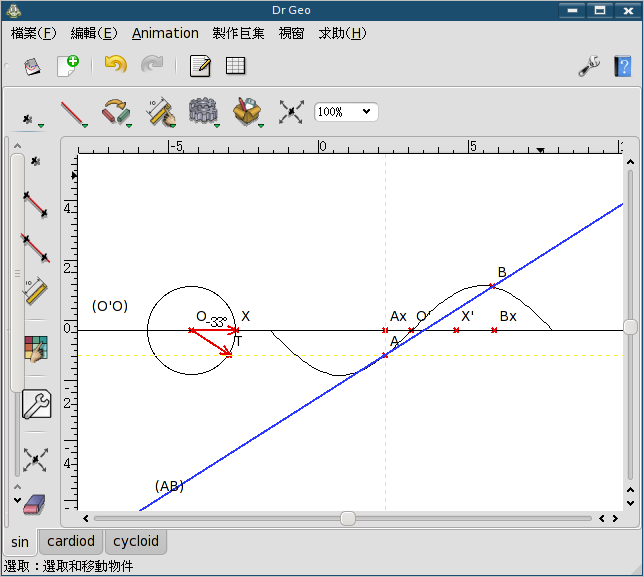
三角函數 sin

特別要注意的是: 這裡度量角度時, 必須度量 向量之間的角度, 因為這樣才會得到 有向角, 圖案才會正確。 如果度量 X,O,T 三點之間的角度, 將得到一個 無向角, 那麼 sin 函數的另一半會跑錯位置。 請自己試試看就知道。

這兩者之間的差別, 有它的教育意義: 這個例子正好可以用來告訴學生: 某些情況下, 有向角其實比無向角更符合自然。

有了量角器, 不僅可以畫三角函數, 還可以畫出很多 "用極座標定義出來的函數"。 例如下圖的 心臟線 (cardioid) r = 1 + cos(th)。 圖中 T 是圓上的自由點, Tx 是它在 X 軸的投影。 次以 O 為原點, 把 Tx 平移 OX, 得到 A, 再以 O 為原點, 把 A 旋轉 (OX,OT) 得到 B。 以 T 為自由點, B 為應變點, 畫出來的軌跡就是心臟線。 仍舊要提醒您, 此類作圖, 度量角度要用 向量之間的有向角。

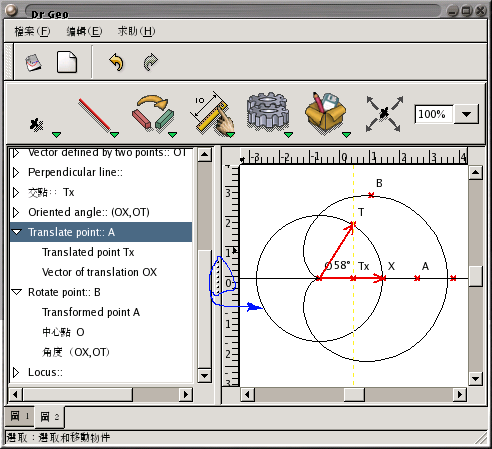
又, 請注意看 drgeo 視窗的最左緣, 中間是不是有一直排七個小點? 如果覺得上面的文字描述不清楚, 可以將這直排小點向右拉, 就可以看到詳細的製圖過程。 (見下圖藍色圈部分) 點下文字旁邊的小三角形, 會展開細節。 建議把製圖過程當中, 一些沒有名字的物件也取上名字, 才容易看懂。

心臟線 cardioid

至於 cycloid

        x = th - sin(th)
        y = 1  - cos(th)

雖然用直角座標寫比較簡單, 但也因為式中有角度與三角函數的加法, 所以需要用量角器。

這個檔案 的三個圖分別是:

  1. sin(x)
  2. cardioid
  3. cycloid

最後這個 cycloid 的做法如下。 為方便作圖, 我們稍微改了一下它的方程式 (其實只是改變 角 th 的相位), 變成:

        x = th - cos(th)
        y = 1  + sin(th)
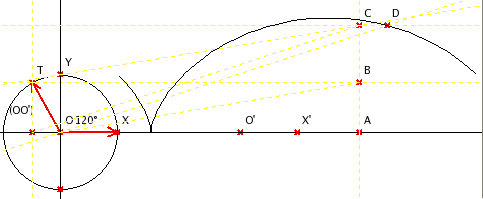
  1. 畫一條水平線 OO', 取線上一點 X 作為單位距離。
  2. 將 O' 平移 OX, 得到點 X'。
  3. 以 O 圓心, OX 為半徑, 畫一個單位圓 Cu。 Cu 交 Y 軸正向於 Y 點。
  4. 在圓 Cu 上取一個自由點 T, 姑且稱 "角 (OX,OT)" 為角 th。
  5. 過 T 畫水平線與垂直線準備使用 sin(th) 與 cos(th)。
  6. 從 X' 出發, 放大 th 倍得到 A, 垂直移動 sin(th) 得到 B, 垂直移動單位長度得到 C, 水平移動 -cos(th) 得到 D。
  7. 以 T 為自變量, D 為應變量, 畫出來的軌跡就是 cycloid。

這裡我用一組組的平行線來移動點; 當然也可以改用向量, 畫面可能會比較乾淨。

cycloid

作業

請畫以下圖形。 你所畫的圖, 必須可以讓使用者任意做 最大幅度 的自由移動/旋轉/縮放/..., 卻仍然要保持題目要求的特性。

  1. 橢圓形
  2. 雙曲線
  3. 給定拋物線的準線 L, 及拋物線上兩點 P 與 Q, 請畫出此拋物線。 (滿足條件的拋物線可能不存在; 也可能有 1 條或 2 條)
  4. 給定拋物線的焦點 F, 及拋物線上兩點 P 與 Q, 請畫出此拋物線。 (滿足條件的拋物線可能不存在; 也可能有 2 條)
  5. (徵求更多有趣的有理函數, 三角函數, 極座標的例子...)

兩題拋物線的解答; 畢其功於一役的橢圓/雙曲線作圖