Graph
請先讀: 表達人事物之間的關係 (為什麼要學 Binary Relation 與 Graph)
更多 Graph 的觀念與術語
被 vertex v 指到的 vertex (vertices), 稱為 v 的 successor(s); 指向 v 的 vertex (vertices), 稱為 v 的 predecessor(s)。 以 「通訊錄」 為例, v 的通訊錄內所有人, 都是 v 的 successors; 通訊錄內含有 v 名字的人, 都是 v 的 predecessors。 至於無向圖, 則不分指出去或指進來, 凡是與 v 有 edge 相連的其他 vertices, 都叫做 v 的 neighbors。 以 「接壤」 為例, 一個國家的 neighbors, 就是與它接壤的鄰居。 (術語往往都很直覺吧!)
從一個 vertex v 指出去的箭頭個數 (其實也就是 v 的 successors 個數), 叫做 v 的 out-degree; 指向 v 的箭頭個數 (其實也就是 v 的 predecessors 個數), 叫做 v 的 in-degree。 以 「通訊錄」 為例, out-degree 越高, 表示通訊錄名單越長; in-degree 越高, 表示人氣越旺 (很多人都將你列在通訊錄內。 小心病毒。) 至於無向圖, 則不分指出去或指進來, 與 v 連線的總數 稱為 v 的 degree。 以 「接壤」 為例, 一個國家的 degree, 就是與它接壤國家的個數。 Q: 「生下」 的 in-degree 或是 out-degree 有何特性? 當然, 現代科技也有可能創造出例外...
兩頭都落在同一個 vertex 上面的 edge, 叫做一個 loop。 這樣的 edge 對這個 vertex 的 degree 貢獻了 2 次。 一般用 graph 描述的問題, 多數都不考慮 loop 可能是因為沒有太大意義, 例如 「握手」; 也可能是因為每個 vertex 都有 loop 所以乾脆全部省略, 例如 「通訊錄」。 Q: 「愛戀」 圖中若出現 loop, 可以用希臘神話裡面的那一種情結來描述?
起點相同, 終點也相同的兩條 edges, 稱為 parallel edges。
一個沒有 loops, 沒有 parallel edges 的圖, 叫做一個 simple graph。 我們一般討論 graphs, 大多只對 simple graphs 有興趣。
degree 為 0 的 vertex 叫做一個 isolated vertex 「接壤」 例中, 每個島國就是一個 isolated vertex。 (但印尼與馬來西亞並不是。)
一連串 edges 依序首尾相接, 不重複經過同一 vertex, 稱為一個 simple path。 若從 vertex a 到 vertex b 有 simple path, 則稱 b is accessible/reachable from a (從 a 可以到達 b) 「溝通」 例中, 若 a 到 b 有 simple path, 則表示 a 講的話, b 可以直接或間接 (透過翻譯) 聽懂。
起點和終點相同的 simple path, 稱為一個 simple cycle。 「溝通」 例中, 一個 simple cycle 上面的每個人, 都可以彼此直接或間接雙向溝通。
一個 undirected graph G 當中, 如果任兩個 vertices 之間都可以找到 simple path, 則稱 G 為 connected (連通圖); 否則稱 G 為 disconnected。 一個 graph 的每一小塊自成 connected 的部分, 稱為一個 connected component。 「接壤」 例中, 歐亞非大陸上的國家構成一個 connected component; 南北美大陸上的國家構成一個 connected component。 印尼雖然不在亞洲大陸上, 但它與馬來西亞接壤, 馬來西亞又與大陸上的國家接壤, 所以印尼也算在同一個 connected component 裡面。
至於一個 directed graph G 是否為 connected, 先忽略它的箭頭方向, 將之視為 undirected graph, 由這個 undirected graph 來判斷原圖 G 是否 connected。
邊上面有數字的圖, 叫做 weighted graph。 例如我們研究都市之間的交通時, 可能會對兩都市之間的票價或行車時間有興趣; 又例如研究國家之間的貿易關係時, 可能會對 「甲國對乙國的出口金額」 有興趣, 這時就會在 edges 上面標上數字。
從圖裡面抓一小塊出來研究
一個問題以 graph 表示, 有時我們只對其中一小部分感興趣, 從原圖 G = (V,E) 當中取出來的一個小圖, 就叫做一個 subgraph。 嚴謹地說, 從 G = (V,E) 的 V 當中隨便取出一些 vertices V', 並且從 E 當中隨便取出一些 "兩端都落在 V' 之內" 的 edges E', 所構成的圖 G' = (V',E') 稱為 G 的一個 subgraph。 「先修」 例中, 所有數學課程之間的擋修關係, 就是原圖的一個 subgraph。
圖的骨架
從一個 connected undirected graph G = (V,E) 當中, 挑一些 edges E' 出來, 與原圖當中所有的 vertices 合起來成為 G' = (V, E') 當然是 G 的一個 subgraph。 如果 G' 滿足: (1) 它是 connected (2) 它沒有 cycle 則稱 G' 為 G 的一個 spanning tree。 也就是要取夠多的 edges 讓它足以張開涵蓋所有的 vertices; 但是又不要取太多 edges 以免造成 cycle。
一個 graph 可能有很多不同的 spanning trees。 但無論如何, 若 G 有 n 個 vertices 則它的每棵 spanning tree 一定恰有 n-1 條 edges 。
一個 weighted connected undirected graph 的所有 spanning trees 當中, edges 總和最小的那些 spanning trees, 稱為 minimal spanning trees。 例如油管佈線, 或網路線的配置, 如果一切以最低成本為考量, 而不考慮替代路線, 可能就喜歡佈成一棵 minimal spanning tree。 這裡說 "minimal" 而不說 "minimum" 主要是因為最小的 spanning tree 可能不只一棵。
一個 disconnected undirected graph G 當然就無法有 spanning tree 了。 但可以為每個 connected component 找出一個 spanning tree, 這些 spanning trees 合起來就稱為 G 的一個 spanning forest。
至於 directed graph G 的 spanning tree 或 spanning forest 呢? 凡是談到 connected 的問題, 一律先將 G 視為 undirected graph 來討論就對了。 因為 spanning tree/spanning forest 的定義當中提到 connected, 所以比照辦理。
特殊的圖
一個 directed graph, 如果裡面完全沒有 cycle, 就叫做一個 directed acyclic graph (DAG)。 「生下」 與 「先修」 必然是 DAG。
沒有 edges, 每個 vertex 都是一個 isolated vertex (因而也都是一個獨立的 connected component), 這種 graph 叫做一個 discrete graph 「生下」 例中, 如果題目範圍內的所有人彼此沒有血緣關係, 那就是一個 discrete graph。
linear graph: ...
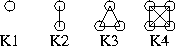 任兩個 vertices 之間都有 edge 相連的 undirected graph 叫做一個
complete graph。 具有 n 個 vertices 的 complete graph,
記做 Kn, 它共有 n(n-1)/2 條 edges。 「溝通」 例中,
如果題目範圍內的所有人都講同一種語言, 那就是一個 complete graph。
右圖分別是 K1, K2, K3 與 K4。
任兩個 vertices 之間都有 edge 相連的 undirected graph 叫做一個
complete graph。 具有 n 個 vertices 的 complete graph,
記做 Kn, 它共有 n(n-1)/2 條 edges。 「溝通」 例中,
如果題目範圍內的所有人都講同一種語言, 那就是一個 complete graph。
右圖分別是 K1, K2, K3 與 K4。
一個 graph, 如果可以找到一種拆法, 把它所有的 vertices 分成兩國, 讓所有的 edges 都橫跨兩國, 也就是同一國內的 vertices 彼此之間都沒有 edges, 則稱此 graph 為 bipartite graph (只允許有 "國際線", 不可有 "國內線") 「愛戀」 一例, 就是一個 bipartite graph。 (除非...)
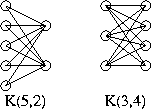 一個 bipartite graph, 如果允許有 edges 的地方都有 edges, 也就是
"國際線" 全滿, 就叫做一個 complete bipartite graph。 若它的兩國各有 m
個與 n 個 vertices, 則將這個 graph 記為 Km,n, 它共有 mn 個
edges。 右圖分別是 K5,2 與 K3,4
一個 bipartite graph, 如果允許有 edges 的地方都有 edges, 也就是
"國際線" 全滿, 就叫做一個 complete bipartite graph。 若它的兩國各有 m
個與 n 個 vertices, 則將這個 graph 記為 Km,n, 它共有 mn 個
edges。 右圖分別是 K5,2 與 K3,4
連得很緊與連得不太緊的 connected graphs
![]() 一個 connected graph 最 "脆弱" 的地方, 是 articulation
point 與 bridge: 前者是 "一拿走, 就會令圖散開的
vertex"; 後者是 "一斷掉, 就會令圖散開的 edge"。 這裡所謂 "散開"
指的是令原來的 connected graph 變成 disconnected graph。 一條
bridge 的兩個端點, 通常都是 articulation points。
(除非端點的 degree 為 1...)
一個 connected graph 最 "脆弱" 的地方, 是 articulation
point 與 bridge: 前者是 "一拿走, 就會令圖散開的
vertex"; 後者是 "一斷掉, 就會令圖散開的 edge"。 這裡所謂 "散開"
指的是令原來的 connected graph 變成 disconnected graph。 一條
bridge 的兩個端點, 通常都是 articulation points。
(除非端點的 degree 為 1...)
「通訊錄」 例中, 班上兩個小圈圈的唯一交集人物就是一個 articulation point; 兩各小圈圈之間唯一有聯絡的兩個人, 就是 bridge。 一個沒有 articulation point (當然也就沒有 bridge) 的 graph 叫做一個 biconnected graph, 也稱為 non-separable graph。 反之, 有 articulation point 的 graph 叫做一個 separable graph。 祝各位畢業以後, 班上的聯絡狀況是一個 biconnected graph, 是一個 non-separable graph。
一個 graph 當中, 每塊大到不能再大的 biconnected subgraph (maximal biconnected subgraph), 叫做一個 biconnected component。 上圖為一個 separable graph, 有 3 個 articulation points, 1 條 bridge, 3 個 biconnected components。
繞得回來與繞不回來的圖
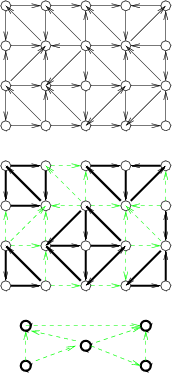 一個 digraph, 如果從每個 vertex 出發, 都有路可以到達其他任何一個
vertex, 就叫做一個 strongly connected graph。 一個 graph
當中, 每塊大到不能再大的 strongly connected subgraph
(maximal strongly connected subgraph), 叫做一個
strongly connected component。
一個 digraph, 如果從每個 vertex 出發, 都有路可以到達其他任何一個
vertex, 就叫做一個 strongly connected graph。 一個 graph
當中, 每塊大到不能再大的 strongly connected subgraph
(maximal strongly connected subgraph), 叫做一個
strongly connected component。
如果將一個 digraph 的所有 strongly connected components 標示出來, 每個 component 以一個大 vertex 取代, 形成一個新的圖, 則這個圖是一個 DAG。 (可以這樣想: digraph 除以 strongly connectedness 等於 DAG。) 上圖為一個 strongly connected graph, 它有 5 個 strongly connected components。 若將每個 strongly connected component 以一個 vertex 取代, 則成最下方的 DAG。
以下尚未整理
Weighted Graph
同構
若 G1 = (V1, E1), G2 = (V2, E2), 且 f 為一個從 V1 到 V2 的 one-to-one correspondence, 並且保留對應 vertices 之間的相鄰關係, 則稱 f 為一個從 G1 到 G2 的 isomorphism. 兩個 graphs 之間如果可以找到 isomorphism, 則稱它們為 isomorphic graphs.
自己到自己的 isomorphism 叫做 automorphism.
Planar Graphs
- 可以被 embed (嵌) 到平面上, 而所有 edges 互不交叉的圖, 叫做 planar graph.
- Kuratowski' Theorem: 一個圖 G 為 non-planar graph <==> G 至少有一個 subgraph 與 K5 或 K3,3 homeomorphic.
- Euler's Formula: 凡是一個 planar graph, 它的 vertices, edges, regions 的個數之間必滿足下列等式: v-e+r=2
- 一個 planar graph 若它沒有 loop 且至少含一個 edge, 則必滿足 3r <= 2e 且 e <= 3v-6. 所以 r 屬於 O(v) 且 e 屬於 O(v).
- 若 G 為一個 planar graph, 則可由 G 定義出它的一個 dual graph (對偶圖) G^d 如下: 在 G 的每個 region r (含 infinite region) 內畫一個 G^d 的 vertex 叫它 r^d; 找出每對相鄰的 regions r1 與 r2 , 及它們之間的分界 edge e, 然後把 r1 與 r2 的 dual vertices r1^d 與 r2^d 用一條 G^d 的 edge 連起來, 命名為 e^d.
- Dual graph 的例子: 地圖上的國家邊界, 它的 dual graph 代表國與國的相鄰關係.
- 本頁最新版網址: https://frdm.cyut.edu.tw/~ckhung/b/dm/graph.php; 您所看到的版本: November 20 2016 22:19:52.
- 作者: 朝陽科技大學 資訊管理系 洪朝貴
- 寶貝你我的地球, 請 減少列印, 多用背面, 丟棄時做垃圾分類。
- 本文件以 Creative Commons Attribution-ShareAlike License 或以 Free Document License 方式公開授權大眾自由複製/修改/散佈。
![[rss feed 圖案]](/~ckhung/i/rss.png)