運算式
運算式/運算子/運算元/優先順序
運算式 expression 在任何程式語言裡面都會出現。 應該說, 沒有學過任何程式語言的小學生也知道運算式是什麼東東。 例如 9 + 8 * 7 + (6 + 5) * (- (4 - 1*2 + 3) ) 就是一個小學生也會算的運算式。 本節談的東西都很簡單, 只是將一些本來就熟悉的東西, 套上有學問的術語而已; 專有名詞的背後, 多半都是你早已熟知的觀念。
+,-,* 等等這些符號, 叫做 運算子 operator。 運算子作用的對象, 叫做 運算元 operand。 例如上式的第一個乘號, 就是一個運算子; 它有兩個運算元 -- 8 與 7。 又例如第二個乘號作用的對象, 是兩個很龐雜的運算元 -- 就是左邊 (6+5) 的結果, 與右邊小括弧內一長串的結果。 左右兩邊必須各自先算完, 才能算乘法。 像這種 "必須先算完" 的東東, 叫做 subexpression 你可以在這個運算式裡面, 找到幾個 subexpressions?
運算子作用的對象, 不見得一定都是兩個運算元。 例如式中最左邊的減號,
作用的對象就只有單獨一個運算元, 也就是 (4-1*2+3) 的結果。
只作用於一個運算元的運算子, 叫做 unary operator
單元運算子。 一般常見的運算子, 多半作用於兩個運算元上, 所以叫做
binary operator 二元運算子。 在許多程式語言裡面,
還有一個有趣的 ternary operator 三元運算子
...?...:... (C 是始祖?)。 問號的左邊是一個 logical
expression 邏輯運算式 它的值如果是 true, 中間那個 subexpression
的答案就是整個運算式的答案; 它的值如果是 false, 右邊那個
subexpression 的答案就是整個運算式的答案。 例如 5>3 ? 17 :
-9 的答案是 17, 而 5<3 ? 17 : -9 的答案是
9。
大家都知道, 在沒有括弧的情況下, "乘方最優先; 先乘除; 後加減"。
這個觀念叫做 operator precedence 運算子優先順序。
至於同樣優先順序的運算子並列時, 先算誰呢? 例如 9-3-2 的答案究竟是 4
還是 8 呢? 2^3^2 究竟是 64 還是 512 呢? 不同的運算子, 有不同的
associativity (結合方向)。 減號的規則是
left-associative 由左向右算; 而乘方的規則卻是
right-associative 由右向左算。 諸如 C, C++ 等語言,
都提供一個 operator precedence table,
其實並不是什麼新的觀念, 只是因為它的運算子太多,
必須將上述規則整理成一個表格而已。 o.p.t.
的功用就是幫助你決定一個 operand, 究竟該被左邊還是右邊的 operator
搶去構成一個 subexpression, 例如 ... * 3 + ...
裡面的 3 應該是誰的運算元? 而 ... * 3 ^ ... 裡面的 3
又應該是誰的運算元? 那 ... - 3 + ... 呢?
請描述你如何查 o.p.t. (而不是靠直覺)
來決定答案。
所以請不要害怕程式語言的複雜運算式,
請用面對加減乘除乘方的輕鬆心情, 看著 o.p.t.
分析你的運算式究竟要如何切割出最先算的 subexpressions 。 練習:
請畫圖分析 char * argv [] 這是一個什麼樣的資料結構?
把運算式的結構畫出來: Expression Tree
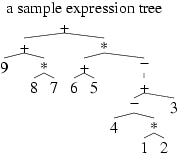 一個運算式很自然地可以畫成一棵樹,
叫做 expression tree 運算式樹。 用 o.p.t. 分析運算式時,
每看出一個 subexpression, 就把這個 subexpression 畫出來, 運算子在上,
運算元在下一字排開, 從運算子向每個運算元畫一條線,
表示這些運算元都歸它用 (而不是歸其他運算子用) 。 隨著分析出來的
subexpression 越來越大, 你的樹也向上越長越高, 最後才算的那個運算子,
將畫在樹的頂端。 再以上面的例子來看, 它的 expression tree 長這樣:
一個運算式很自然地可以畫成一棵樹,
叫做 expression tree 運算式樹。 用 o.p.t. 分析運算式時,
每看出一個 subexpression, 就把這個 subexpression 畫出來, 運算子在上,
運算元在下一字排開, 從運算子向每個運算元畫一條線,
表示這些運算元都歸它用 (而不是歸其他運算子用) 。 隨著分析出來的
subexpression 越來越大, 你的樹也向上越長越高, 最後才算的那個運算子,
將畫在樹的頂端。 再以上面的例子來看, 它的 expression tree 長這樣:
有了 expression tree, 就可以不必小括弧, 不必再查 o.p.t., 很清楚地直接可以看出誰先算誰後算。 一個 operator 的所有 operands 必須全部先算完, 才能算這個 operator。 也就是由樹的下面往上面算。
postfix notation
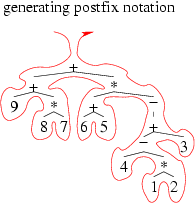 沿著一棵 expression
tree 的外圍繞一圈, 把一路上看到的運算子與最底層運算元全部印出來,
但遵循以下原則: 每個運算子列印的時機, 在最後一次見到它時,
也就是即將離開它所帶領的 subexpression 時。
按照這個方式寫出來的運算式, 叫做 postfix notation 或
reverse polish notation。 例如本篇當中最早的例子, 它的
postfix notation 就是:
沿著一棵 expression
tree 的外圍繞一圈, 把一路上看到的運算子與最底層運算元全部印出來,
但遵循以下原則: 每個運算子列印的時機, 在最後一次見到它時,
也就是即將離開它所帶領的 subexpression 時。
按照這個方式寫出來的運算式, 叫做 postfix notation 或
reverse polish notation。 例如本篇當中最早的例子, 它的
postfix notation 就是: 9 8 7 * + 6 5 + 4 1 2 * - 3 + 負號 *
+ 注意原來運算式當中的第二個減號, 因為它是一個 unary operator,
所以我們寫成 "負號" 以便與二元的減號區別。
一個好好的運算式, 為什麼要寫成 postfix notation? 第一, 這樣就不需要小括弧了。 第二, 如果想要寫一個程式求運算式的值, 其實 postfix notation 比普通的寫法更容易處理。 我們只需要一個 stack, 用以下規則即可運算:
- 遇到運算元就 push
- 遇到一個 n 元運算子就做 n 次 pop, 抓出 n 個運算元加以計算, 再將計算結果 push 回去
stack 2
grows 1 1 2 3
^ 7 5 4 4 4 4 2 2 5 -5
| 8 8 56 6 6 11 11 11 11 11 11 11 11 11 -55
| 9 9 9 9 65 65 65 65 65 65 65 65 65 65 65 65 65 10
+---> time flows
相對於 postfix notation, 傳統的運算式叫做 infix notation, 顧名思義就是將運算子放在中間。 可想而知, 另外有一種寫法叫做 prefix notation, 與 postfix 正好相反。 由以上可知, 處理 postfix 比起處理可以有層層小括弧的 infix, 要簡單多了。
拿到一個 postfix notation 寫法的運算式, 要如何將它的 infix notation 寫出來呢? 一樣需要一個 stack 來裝運算過程, 且做法與上述求值步驟幾乎類似, 只不過這回 stack 裡面裝的不是中間產生的數字, 而是一棵棵的 subexpression 的 expression tree:
- 遇到運算元就 push
- 遇到一個 n 元運算子就做 n 次 pop, 抓出 n 個 subexpression 將它們串到運算子底下變成單獨一棵 expression tree, 再將這棵 expression tree push 回去。
- 本頁最新版網址: https://frdm.cyut.edu.tw/~ckhung/b/pr/expression.php; 您所看到的版本: February 14 2012 10:32:25.
- 作者: 朝陽科技大學 資訊管理系 洪朝貴
- 寶貝你我的地球, 請 減少列印, 多用背面, 丟棄時做垃圾分類。
- 本文件以 Creative Commons Attribution-ShareAlike License 或以 Free Document License 方式公開授權大眾自由複製/修改/散佈。
![[rss feed 圖案]](/~ckhung/i/rss.png)